K***i
ehm. Abiunity Nutzer
19.08.2021 um 13:41 Uhr
Kann mir vllt jemand die Abbildung hier erklären?
Die Abbildung zeigt die Zustandsdichte dn/dE in einem fermi gas bei T= 0 Kelvin. Aber warum sieht die Kurve so aus ? Und was würde passieren wenn die Temperatur steigen würde ?
Danke
Die Abbildung zeigt die Zustandsdichte dn/dE in einem fermi gas bei T= 0 Kelvin. Aber warum sieht die Kurve so aus ? Und was würde passieren wenn die Temperatur steigen würde ?
Danke
Für ein frei bewegliches Teilchen, z.B. ein Fermi-Gas aus Elektronen, gilt ja für die kinetische Energie

Betrachtet man das Elektron als Welle, so gilt für dessen Impuls

also
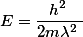
Nun kommt eine Quantisierung: Befinden sich die Elektronen in einem Kristall mit einem periodischen Kristallgitter, so sind nicht mehr alle Wellenlängen möglich, sondern nur noch diskrete Werte, die zur Periodizität des Gitters passen. Alle anderen Wellenlängen würden sich weginterferieren. Zählt man so alle Wellenlängenwerte
möglich, sondern nur noch diskrete Werte, die zur Periodizität des Gitters passen. Alle anderen Wellenlängen würden sich weginterferieren. Zählt man so alle Wellenlängenwerte  , die in einem bestimmten Kristallvolumen V möglich sind, und rechnet sie mit der obigen Formel für E um, so erhält man dass es
, die in einem bestimmten Kristallvolumen V möglich sind, und rechnet sie mit der obigen Formel für E um, so erhält man dass es
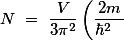^{\frac{3}{2}}E^{\frac{3}{2}})
Werte pro Volumen gibt. (Die genaue Herleitung ist zu umfangreich, um sie hier einzuschreiben).
In deinem Bild ist die Zustandsdichte dn/dE gezeigt, also wieviele Werte es pro Volumen und pro Energieintervall gibt. Wenn du die Formel für nach E ableitest, erhältst du
nach E ableitest, erhältst du
 . Das ist die abgebildete Parabel.
. Das ist die abgebildete Parabel.
Nun kommt noch das Pauli-Prizip hinzu: Bei Fermionen darf kein Zustand, also keine Kombination aus Energie, Wellenlänge und Spinrichtung, mehrmals besetzt sein. Jedes Elektron kann also nur 1 Punkt innerhalb der abgeildeten Parabel besetzen. Alle weiteren Elektronen füllen also diese Parabel wie Sekt in einem Sektglas von unten nach (geringste Energie) nach oben (höchste Energie) auf. Die höchste Energie bildet eine scharfe Kante (wie eine Wasseroberfläche) und die nennt man die Fermi-Energie .
.
Das gilt bei Temperatur T=0. Erhöht man die Temperatur, so geraten die Teilchen in Schwingung. Die Teilchen unterhalb der Fermi-Energie können sich aber nicht bewegen, da der Nachbarzustand bereits durch ein anderes Elektron besetzt ist. Lediglich an der Oberfläche kann es "brodeln", weil dort noch freie Zustände vorhanden sind. Das bewirkt, dass bei T > 0 auch einige Zustände oberhalb von besetzt werden und einige Zustände unterhalb
besetzt werden und einige Zustände unterhalb  unbesetzt bleiben.
unbesetzt bleiben.
Betrachtet man das Elektron als Welle, so gilt für dessen Impuls
also
Nun kommt eine Quantisierung: Befinden sich die Elektronen in einem Kristall mit einem periodischen Kristallgitter, so sind nicht mehr alle Wellenlängen
Werte pro Volumen gibt. (Die genaue Herleitung ist zu umfangreich, um sie hier einzuschreiben).
In deinem Bild ist die Zustandsdichte dn/dE gezeigt, also wieviele Werte es pro Volumen und pro Energieintervall gibt. Wenn du die Formel für
Nun kommt noch das Pauli-Prizip hinzu: Bei Fermionen darf kein Zustand, also keine Kombination aus Energie, Wellenlänge und Spinrichtung, mehrmals besetzt sein. Jedes Elektron kann also nur 1 Punkt innerhalb der abgeildeten Parabel besetzen. Alle weiteren Elektronen füllen also diese Parabel wie Sekt in einem Sektglas von unten nach (geringste Energie) nach oben (höchste Energie) auf. Die höchste Energie bildet eine scharfe Kante (wie eine Wasseroberfläche) und die nennt man die Fermi-Energie
Das gilt bei Temperatur T=0. Erhöht man die Temperatur, so geraten die Teilchen in Schwingung. Die Teilchen unterhalb der Fermi-Energie können sich aber nicht bewegen, da der Nachbarzustand bereits durch ein anderes Elektron besetzt ist. Lediglich an der Oberfläche kann es "brodeln", weil dort noch freie Zustände vorhanden sind. Das bewirkt, dass bei T > 0 auch einige Zustände oberhalb von






